What Is Quantum Computing and Who Uses It

Y. Navatej1, Dr. T. Ravindar1

1School of Technology, Woxsen University, Hyderabad, India

Abstract

Quantum computers will be radical advances in computing power that use the laws of quantum physics like superposition and entanglement, to informational processing in an entirely new manner. In contrast to classical computers, which operate on bits being fixed as 0 or 1, quantum computers operate with qubits that are able to be in a superposition of states and therefore are able to explore the huge space of solutions in parallel. The ability will make quantum computing a hopeful tool to solve complex problems that classical machines cannot, such as cryptography, molecular simulation, sophisticated optimization, and big data analysis [1].

Key words: Quantum, Quantum computer, Quibit, Cryptography, Quantum physics

1. Introduction:

What is quantum computing?

Let us imagine the tiny particles inside atoms which can do strange things like being present in two places at once or being mysteriously linked even far apart. Quantum computers utilizes these strange properties to build “qubits,” which are like super powerful bits unlike a normal computer bit is either 0 or 1. A qubit can be 0 and 1 at the same time (A spinning coin has both heads and tails while in the air). It can also become entangled with other qubits so that they act together in special ways. By using superposition and entanglement, a quantum computer can try many possibilities all at once. In simple terms, quantum computers do computations in a totally different way from everyday computers, aiming to solve problems that are too big and too slow for normal machines. Researchers state this makes quantum computing a frontier of science that brings together physics, engineering, and computer science [1].

1. Why are quantum computers required?

Our normal computers excel at a lot of things, however they have a hard time with certain specialized problems. As an illustration, it is virtually unfeasible to break large secret codes (factor large numbers) with a regular PC - the known fastest method would take longer than the universe has existed. Classical machines are also extremely difficult to simulate exact behavior of complex molecules or materials. These tasks become exponentially more complicated with their increase in size [2]. In finance, quantum computing helps to determine the absolute optimal combination of investments (portfolio optimization) one would need to examine an immense number of combinations where as the classical algorithms accept good enough shortcuts instead. In brief,

issues such as cryptography, database search in large data sets, sophisticated optimization and molecular

chemistry simulations are extremely challenging on conventional computers, as the task scales far too quickly with the size.

1. Who uses Quantum computers nowadays?

Universities, government labs, and a combination of large corporations are all leaping into quantum. Big tech names, including IBM, Google, Microsoft, and Amazon, have constructed quantum computers or provide quantum as a service computing. By way of illustration, IBM and Google have invested billions of dollars in quantum computing to crack highly difficult problems, Microsoft looking into how to create more stable qubits [3]. There are also startups, such as D-Wave, Rigetti, and IonQ, which sell quantum devices and services (D-Wave specalizes in a particular type of quantum annealing). Even national laboratories and government agencies: the U.S. Department of Energy and Defense, Canada’s quantum institutes, China’s research centers, and the European Commission all fund quantum projects. and Universities worldwide are racing to experiment with quantum chips often via cloud access. In fact, one survey of quantum research calls it an “interdisciplinary frontier” involving computer science, physics, chemistry and engineering [3].

1. What are they using quantum computers for?

Everyone is exploring different ideas and the big hope lies in chemistry and materials: Quantum computers can directly simulate molecules and chemical reactions in the language of quantum physics assisting design new drugs and better batteries. For example, scientists built a “pipeline” for real drug research using quantum simulation of molecules and how bonds break. In finance and logistics, firms test the performance of quantum algorithms for optimization where as banks are experimenting with quantum methods to pick portfolios that balance risk and return. Automobile, airline, and energy companies look at quantum to optimize routes and power grids often using a hybrid of quantum and normal computing. Another area is machine learning and AI: some researchers try to speed up certain learning tasks using quantum tricks (though this is very early stage). Finally, an important theoretical application is cryptography where the quantum computers could in principle break some encryption (like RSA codes) by factoring large numbers quickly. This has made security agencies very interested in both quantum computing and new “quantum-safe” encryption [1].

1. How the quantum computers succeed where classical ones fail?

The key is quantum parallelism, where a qubit’s ability to be in both 0 and 1 states lets a quantum computer test many possibilities at once, in some special tasks, this leads to huge speed-ups. Shor’s quantum algorithm can factor numbers exponentially faster than the best known classical method which means a quantum computer could crack certain codes in minutes that would take a classical supercomputer ages [1, 5]. Another example is Google’s 53-qubit “Sycamore” chip which performed a specific calculation in 200 seconds that they claimed would take for a state of the art classical supercomputer 10,000 years, a milestone called “quantum supremacy” [6, 7]. In research, a 127-qubit quantum  processor  recently  solved  a

problem with strong quantum entanglement where as the leading classical approximations failed. In

plain terms, the quantum computer got the right solution on a problem however the ordinary methods couldn’t solve it. These results suggest that quantum machines can tackle complex simulations related to development of new materials and nuclear physics that appears to be impossible for classical machines. A D-Wave’s quantum annealer has shown a promising output on certain quadratic problems and real energy scheduling tasks that are sometimes finding good solutions faster than classic solvers. In all these cases, quantum processors use their quantum physics to search and compute in processes that a no standard computer can mimic.

1. Industry, academia and government examples:

Several firms are already testing the quantum supremacy capabilities on the quantum chip, for instance, Google. IBM produces 127-qubit computers and allows scientists to conduct experiments on its computers. Portfolio tests have been done with quantum algorithms on an IBM and D-Wave machine

by banks and finance companies such as JPMorgan Chase. Pharmaceutical companies such as Roche and Biogen teams up with startups to model molecules on quantum computers. Volkswagen among others attempted quantum traffic routing with the annealer of D-Wave [4]. Academia is full of activity, too: thousands of papers are published on quantum algorithms and experiments, and most university labs have access to small quantum computers and clouds. Quantum testbeds were being used by chemists and material scientists as well as machine learning researchers to experiment with new algorithms. Governments are supporting numerous quantum efforts: the US, EU, China and Canada all have begun

multi-year quantum initiatives. Quantum hardware is also housed in national labs like Oak Ridge,

Argonne in the U.S. and also collaborate with universities to tackle large scientific issues. Although in the majority of situations, the outcomes remain prototype, research, these demonstrations indicate a wide spread interest: almost every country and large tech corporation currently has a quantum strategy.

1. What today’s quantum computers are lacking?

It is important to be clear about the current quantum machines are still very limited with typically only a few dozen or at most a few hundred qubits. These qubits are very fragile and noisy, they lose their quantum state easily. Scientists say that this noise is the “greatest impediment” right now [3]. Error correction methods exist, but they require thousands of physical qubits to make one reliable qubit, which is out of reach and in practice most real world problems are still too large for today’s quantum hardware. Studies have found that for many industrial tasks, a quantum computer would need far more qubits than we have now, for example when researchers tried D-Wave’s machine on a simplified energy optimization problem, it solved it but still lagged behind the best classical solver [4]. In finance, early tests of quantum portfolio algorithms reached answers close to the classical ones only when the quantum computer was small; scaling them up without noise is a challenge and in short, while quantum computers show potential, they cannot yet beat classical computers in general, only in carefully chosen cases.

1. Frameworks for quantum computing:

Quantum computing frameworks provide tools, libraries, and platforms to design, simulate, and run quantum algorithms.

Table1: Some prominent quantum computing frameworks

Table 2: Comparison of Bit and Qubit [8-10]

1. How might quantum computing disrupt current encryption methods?

The steep development of the branch of quantum computing technology raises a number of serious questions on its theoretical backgrounds, efficiency restrictions, and impact on society. One key area of inquiry concerns about the future of cryptographic security: How can quantum computing undermine the current directions in cryptographic security, especially the knapsacks based on the intractability of integer factorization and discrete logarithms (like RSA and ECC)? This leads to the next issue which

has to be discussed the necessity to develop and standardize post-quantum cryptography algorithms that resistance to quantum attacks [11].

One more interesting question touches those of computational paradigm: What areas of computational advantage will quantum proven most effective, optimization, simulation, machine learning, or others, and what performance benchmarks would characterize usefulness of quantum computation beyond the (artificial and short-lived) demonstrations of supremacy? [9]. A hardware aspect is no less essential: What are the best routes to scalable, fault tolerant quantum computers, and how can error correction be designed in such a way as to keep overhead to a minimum, without sacrificing coherence? Those questions highlight the conflict between the theoretical potential of exponential speedup and real engineering difficulties that remain. It is also ethical and, to some extent, socially important to ask: How should access to quantum computing resources be regulated, to avoid technological injustice or abuse, even since they can crack many commonly used cryptographic systems? It is critical to discuss these aspects as they can guide research priorities and policy formations in an area that would transform computation, security and the concept of privacy at the global level.

1. Step by step breakdown of how a quantum algorithm solves a specific problem:

The quantum-computing paradigm presents a basic new model of discussing solutions to a subset of problems taking advantage of quantum superposition, entanglement and quantum interference to search solution spaces more effectively than classical methods. The power of this is demonstrated by Shor, the first comprehensive quantum algorithm to factor integers, which, step-by-step, provides exponential speedup over any known classical algorithm. The algorithm is given a composite integer N, the factorization problem is reduced to a problem solving a function period of the function f(x)=ax mod N where 0 Traditionally calculating ???? would take exponential time; instead quantum algorithm prepares a superposition of all the possible values of 10x in a register and performs a modular exponentiation operator that entangles the two states, the input and the output which would encode the periodicity of ???? ( ???? ) f(x) into the quantum state amplitude [9, 14].

Then a quantum Fourier transform (QFT) is performed on the input register to map the periodicity in the computational basis to peaks in the frequency domain (at the reciprocal of the period). The transformed state is then measured, which returns a value which is with high probability close to a rational approximation of ???? / ???? k/r, out of which ???? may be deduced by classical post-processing like continued fraction algorithm. After all, having ???? at hand, it is easy to find the greatest common divisor of ???? E ????/2 ± 1a r/2 ±1 and ???? to expose a non-trivial factor of ????. This serial interaction between quantum parallelism, interference and measurement is a good example of why quantum algorithms can be much more efficient at some computational problems than an equivalent circuit of classical computers, wherein we assume coherent control of qubits and acceptably small error rates are possible at circuit depths of the same order [9]. These algorithms do not just demonstrate the potential of quantum advantage, but also make it possible to go further to build fault-tolerant architectures to achieve the same promise on a larger scale.

Table 3: Flowchart showing classical vs quantum computing workflow

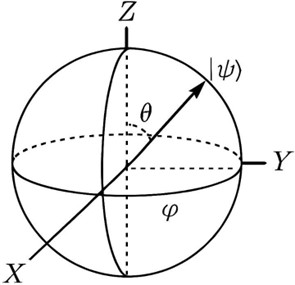Bloch sphere to represent different states of qubits

Important Aspects on the Bloch Sphere:

1. Sphere:

Denotes the states of a single qubit, i.e. all the pure states of that qubit. Each of the points on the surface has a distinct qubit state associated to it.

1. Axes (X, Y, Z):

Diagonal - an articulated plane, which is established as standard Cartesian axes:

Z axis: Points up and down, the north pole enters in |0⟩ (zero qubit state) and the south pole enters in

|1⟩ (one qubit state). X-axis and Y-axis: perpendicular to the Z, on the plane which produces the equator.

1. State Vector (Vector- One Arrow):

An angle that goes to the center of the surface to another point. Shows the precise quantum state that the qubit is on. The state is at the tip of the vector and the coordinates (zero angles 0 and 0) are defined.

1. Angles: θ (Theta) and φ (Phi):

Theta (θ): The angle from the positive z-Axis. Continues to vary between 0 (north pole), and 2 pi (south pole). Phi (φ) Azimuthal angle depicted in the X-Y plane by X-axis. Between 0-2pi (all way round the equator).

1. Labeled Poles:

|0⟩ (North pole): the archaetypical zero state.

|1⟩ (South Pole): The so-called one state.

What does the Schematic Mean?

Information of any pure quantum state can be presented as:

∣ψ⟩ = cos(2θ)∣0⟩+eiϕsin(2θ)∣1⟩

Always, the pure states have the state vector of length 1. A rotation in the θ direction shifts the end of the vector between the two poles (it changes the probability amplitude between |0⟩ and |1⟩). A rotation of the 2-D sphere with the angle of changing 0 rotates the vector about the Z-axis (influencing the phase between |0⟩ and |1⟩).

What the elements mean:

The schematic visually encodes all possible pure quantum states of a single qubit. By identifying the endpoint of the vector through θ and φ you can specifically determine the state of the composition and the phase. The Bloch sphere is an impressive tool in explaining and manipulating quantum bits in the quantum computing and quantum information science sectors.

Qubit Quantum Coin Flipping: A quantum coin flipping protocol is a cryptographic protocol that allows two distant parties to flip a fair coin (i.e. generate a random bit) in such a manner that no participant can tamper with the result to their advantage, even when both sides collude. Quantum coin flipping, unlike classical coin flipping, operates on qubits, quantum bits to enhance the security and decrease the cheating potential [8].

What Is The Concept of Qubits Use: Preparation One party (Alice) prepares a qubit into one of a number of non-orthogonal quantum states which can represent her coin choice (e.g. |0⟩ or |+⟩ = (|00⟩ +

|11⟩)/sqrt(2). These two states cannot be perfectly distinguished and accordingly the other party (Bob) will not know what the specific state is without disturbing it. Alice transmits the qubit to Bob here he carries out a measurement to make a guess.

Verification and Outcome: Verification and Outcome based on the measurement through Bob and subsequent classical communication gives an agreement of the outcome of the coin flip between both parties. The rules of Quantum mechanics ensure that any dishonest behaviour by one side (i.e. measuring prematurely or faking the prepared state) creates disturbances that can be detected. This inherent uncertainty guarantees a fairness which goes beyond the classical frontiers. The example shows how the principles of quantum information of superposition and uncertainty in measuring that quantum objects are subject, allow trusted randomness generation key to secure protocols in quantum cryptography [8].

1. Quantum advantage:

The demonstration that a quantum device can solve a well defined computational problem faster than the best known classical algorithms is an important milestone on the quantum computing research

journey, but requiring it to succeed under a severe test with solid supporting data. Quantum advantage must be made plausible with regard to experimental findings being compared to the most efficient classical methods known at that point, subject to hardware shortcomings, errors and even the problem formulations themselves, which have occasionally been engineered to artificially tilt the balance in favor of quantum architectures [9]. To give an example, the first Google demonstration of quantum advantage (Google Sycamore 2019) postulated 200 seconds to complete a task that would apparently have taken seven years (approximately 300,000 years) of classical supercomputation resources; an analysis done later, indicated that more efficient classical simulation might produce a large reduction in time [14, 12]. Therefore, the independent replication, open methodology, and extended comparisons with the state of the art classical solvers are essential to prove the claims of the quantum advantage and prevent the overstatement of abilities. In addition, statistical confidence in their results, error reduction strategies, and scaling factors have to be well documented so that surveyed performance could indeed be characterized by maxims of quantum mechanics, not by experimental artifacts [13]. A uniform protocol of proving the quantum advantage claims (just as there exist reproducibility standards in other domains of computational science) would help in developing a sense of credibility and hasten developments in the field.

1. Quantum readiness checklist:

A pragmatic quantum readiness checklist established a systematic model to measure the situative quantum readiness of an organization to incorporate quantum computing technologies in three dimensions of importance: error correction, scalability, and hybrid strategies. First, strong quantum error correction (QEC) strategies will be needed, because the current quantum processors are subject to decoherence and gate errors, which undermine the fidelity of computations; the organizations need to assess whether the platforms under consideration support surface codes, otherwise some other QEC mechanism that has demonstrated a logical error rate that can go below the fault tolerance threshold [14, 15]. Second, to address problems that are industry scale, scalability is a key that must be addressed; readiness involves a study of connectivity in qubits, reproducibility of fabrication, and roadmaps into architecture, in which improving upon thousands and millions of physical qubits is possible in the long term scenario [9]. Third, near term utility with noisy intermediate scale quantum (NISQ) systems can be achieved by offloading to classical processors some of the computation, in hybrid quantumclassical paradigms like variational quantum eigensolvers (VQE), or quantum approximate optimization algorithms (QAOA), and employing quantum advantage wherever possible [16, 17]. Collectively, this checklist presents a scientifically supported manual to help the stakeholders ascertain the gaps and opportunities within their quantum adoption strategy keeping in view the changing circumstances within the sphere.

1. Quantum supremacy and optimization with the sycamore processor of google:

Quantum networking, however, has delivered a much more pronounced impact in terms of promising potential exponential speedups in computation in certain problems since the quantum era began, but never did it reach a quantified milestone, as Google recently did, in 2019 [7, 18], by performing quantum supremacy with its Sycamore quantum processor, a 53-qubit system. This case study examines the problem solving process that led to this mile stone, with scientific and industrial implications to computation. The problem being solved was sampling of a pseudo-random quantum circuit relative to the classical supercomputer after a certain number of qubits and circuit depths, which becomes intractable. The initial benchmark problem chosen by Google engineers was an output distribution sampling of a randomly generated quantum circuit of depth 20 on a lattice of superconducting qubits [7, 18]. The issue was selected to be able to execute with relatively high effectiveness on quantum hardware and on the other hand, on classical simulation, the cost cannot be meaningfully estimated.

The image part w ith relationship ID rId10 w as not found in the file.

The solution was done in a number of steps. Then, hardware characterization was applied to ensure the qubits were range and calibrated to minimize gate errors and cross talk, with the cumulative fidelity across the circuit still being high enough to sustain a computational advantage. Then the team designed and ran random quantum circuits on Sycamore to get millions of output bitstrings. To test whether they were right they carried out a cross entropy benchmarking the distribution of the experimentally measured output with the theoretically ideal distribution; the resulting cross entropy score proved high enough to be confident the quantum device was drawing output samples to the right same distribution. At the same time, the classical simulation of the same circuits was also tried with state of the art high performance computing resources and its free command of petabytes of memory and thousands of CPU hours was not able to compete with the quantum device in its cost or time. Google claimed that Sycamore undertook the sampling process within 200 seconds, whereas estimates showed that conventional supercomputers would have taken a classical quantum computer up to 10,000 years to complete the same calculation, whereas clear quantum advantage was evident on this particular task [7, 18].

This recipe of building block by block the representation of a computationally hard problem, then implementing the hardware up to the highest fidelity possible, then implementing the quantum circuit, then proving that the circuit was correct with a statistical benchmark to assure it works, and comparing to a classical limit is the roadmap to proving quantum advantage in more real world applications like optimization, cryptography, and materials simulation. Unthough the benchmark problem itself does not have any direct industry application, the approach demonstrates the use of quantum hardware and algorithm co-design as two ways to discover new regimens of performance that are inaccessible using classical techniques. The next effort of future research is now directed to extending the techniques to useful problems in optimization, in which hybrid quantum classical solvers have the potential to offer useful near term opportunities in quantum logistics, finance, and machine learning.

1. Future outlook

The field is moving fast with many experts expecting quantum hardware to improve in the coming years. Google and others projects double the exponential growth in quantum power meaning each advance will make classical simulation much harder [7]. New ideas in qubit design like Microsoft’s

topological qubits could lead to more stable machines as researchers are also developing hybrid approaches that combine quantum and classical computing to get better results today. However, it will still take time before we have the error corrected large scale quantum computers. In the near term, the emphasis is on “quantum advantage” - finding any real problem where a quantum device outperforms classical ones. Nature reports that recent experiments have become “foundational tools” for the near term applications which means we are taking the first steps: scientists have shown devices solving toy problems beyond classical reach, and now they are working on scaling those to useful tasks [3]. So while  quantum  computing  isn’t  yet

improving your smartphone and making all traditional problems easy, however it is a real technology

being tested now. In a few years we may see it speeding up new drug discoveries, solving tougher

puzzles in physics, and reshaping cybersecurity, at present, the main objective is understanding and benchmarking quantum machines, a lot of labs and companies are doing exactly that with studies and experiments. In summary quantum computing is an exciting and emerging field. It promises to solve problems beyond the reach of classical computers and we already see early users in science and industry. However it remains as an evolving technology with much more research needed before its full power is unleashed.

References

1. 1. Montanaro, A. (2016). Quantum algorithms: An overview. npj Quantum Information, 2, Article 15023.
   2. Wang, Y., & Liu, H. (2022). Quantum Computing in a Statistical Context. Annual Review of Statistics and Its Application, 9, 479–504.
   3. Kim, Y., et al. (2023). Evidence for the utility of quantum computing before fault tolerance. Nature, 618, 500–505.
   4. Quinton, F. A., et al. (2025). Quantum annealing applications, challenges and limitations for optimisation problems compared to classical solvers. Scientific Reports, 15, 12733.
   5. Skosana, U., & Tame, M. (2021). Demonstration of Shor’s factoring algorithm for N = 21 on IBM quantum processors. Scientific Reports, 11, 16599.
   6. Annoni, M., et al. (2023). Best practices for portfolio optimization by quantum computing, experimented on real quantum devices. Scientific Reports, 13, 19434.
   7. Arute, F., et al. (2019). Quantum supremacy using a programmable superconducting processor. Nature, 574, 505–510.
   8. Nielsen et. al. (2010).Quantum Computation and Quantum Information, Cambridge University Press.
   9. Preskill, J. Quantum Computing in the NISQ era and beyond, Quantum, 2018.
   10. Ladd et al., (2010). Quantum computers, Nature.
   11. Bernstein, D. J., & Lange, T. (2017). Post-quantum cryptography. Nature, 549(7671), 188–194.
   12. Pan, Z., & Zhang, Y. (2021). Simulating the Sycamore quantum supremacy circuits. Quantum, 5, 559.
   13. Harrow, A. W., & Montanaro, A. (2017). Quantum computational supremacy. Nature, 549(7671), 203–209.
   14. Fowler, A. G., et al. (2012). Surface codes: Towards practical large-scale quantum computation.

Physical Review A, 86(3), 032324.

1. 1. Terhal, B. M. (2015). Quantum error correction for quantum memories. Reviews of Modern Physics, 87(2), 307–346.
   2. Peruzzo, A., McClean, J., Shadbolt, P., Yung, M.-H., Zhou, X.-Q., Love, P. J., Aspuru-Guzik, A., & O’Brien, J. L. (2014). A variational eigenvalue solver on a photonic quantum processor. Nature Communications, 5, 4213.
   3. Farhi, E., Goldstone, J., & Gutmann, S. (2014). A Quantum Approximate Optimization Algorithm. arXiv preprint arXiv:1411.4028.
   4. Google AI Quantum and Collaborators, (2019). Quantum supremacy using a programmable superconducting processor." Nature 574, 505–510.